Nih Rumus Pitagoras Segitiga Siku-Siku Beserta Contoh Soalnya
Jika dipikir-pikir ini materi Segitiga Siku-Siku sudah kita dapatkan mulai dari bangku SD,SMP/Mts bahkan di SMA/SMK juga masih memerlukan rumus ini.
Matematika atau bisa disebut dengan materi rumus sejati ini tidak bisa di rubah lagi, karena sifatnya adalah tetap dan biasanya mengalami kemajuan seiring berkembangnya jaman, banyak siswa /siswi yang masih belum tahu cara menghitung Rumus Pitagoras Segitiga Siku-Siku ini karena memang mereka belum tahu atau bahkan lupa bagaimana Rumus Pitagoras Segitiga Siku-Siku itu.
Ini wajar saja kok, karena memang kita menerima materi tidak hanya matematika saja, banyak materi yang lain juga, jadi ketika harus mengingat semua, jadinya lupa semua deh, hehehe, semua tergantung pada kemampuan daya mengingat siswa dan siswa, bahkan ada yang mudah sekali menerima pelajaran matematika / berhitung, dan ada juga yang susah sekali, bagi yang suka dengan matematika saya yakin kalau ditanya Rumus Pitagoras Segitiga Siku-Siku akan mudah sekali menjawabnya, tapi bagaimana dengan anda yang belum tahu? pasti cuma tengok kanan dan kiri kan, tetapi anda tidak usah kawatir disini kalian akan mendapatkan penjelasan lengkap dari materi sekolah yang akan membantu anda menemukan teka-teki mengenai Rumus Pitagoras Segitiga Siku-Siku beserta Contoh Soalnya.
Rumus pitagoras adalah sebuah rumus yang digunakan untuk mencari salah satu panjang sisi segitiga siku-siku yang belum diketahui. Jadi rumus ini akan berlaku jika ada 2 panjang sisi yang diketahui nilainya dan hanya satu sisi yang belum diketahui nilainya. Rumus pitagoras ditemukan oleh seorang ahli matematika asal Yunani yang bernama Pythagoras dan untuk mengenang nama penemunya rumus ini dinamakan dengan Rumus Pythagoras.
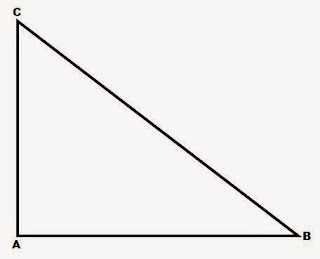
Pada kesempatan ini saya akan mengulas mengenai rumus pitagoras untuk segitiga siku-siku. Segitiga siku-siku memliki 1 sisi tegak, 1 sisi datar, dan 1 sisi miring. Untuk mencari panjang salah satu sisi ini dapat menggunakan rumus pitagoras segitiga siku-siku dimana syaratnya harus ada dua sisi yang nilainya diketahui, entah itu sisi tegak, sisi datar, atau sisi miring. Perhatikan gambar segitiga siku-siku di bawah ini:
Ada sebuah segitiga siku-siku ABC. Ada 3 sisi yang membentuknya, yaitu sisi AB, sisi BC, dan sisi CA. Rumus pythagoras yang berlaku untuk segitiga tersebut adalah sebagai berikut:
BC2 = AB2 + AC2
Jadi untuk mencari panjang BC, maka panjang AB dan panjang AC harus diketahui, supaya rumus ini dapat dikerjakan. Begitupun sebaliknya jika yang akan dicari adalah panjang AB atau panjang AC. [Baca : Rumus Luas dan Keliling Segitiga]
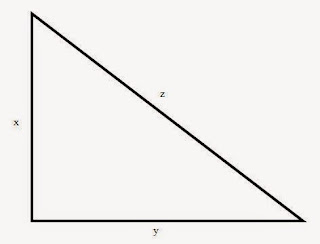
Dalam sebuah soal, terkadang gambar dan pertanyaannya berbeda dari yang di atas. Bentuk lain gambarnya adalah sebagai berikut:
Meskipun menggunakan gambar yang sama, tetapi struktur rumus pitagoras tetap sama. Yang berubah adalah variable-nya, bukan rumusnya. Untuk bentuk gambar sola seperti di atas, rumus pythagoras memiliki bentuk seperti ini:
z2 = x2 + y2
Rumus di atas adalah untuk mencari panjang sisi z. Jika akan mencari panjang sisi x, rumus yang dipakai adalah sebagai berikut:
x2 = z2 - y2
Untuk mencari panjang sisi y, rumus yang dipakai adalah sebagai berikut:
y2 = z2 - x2
Dari ketiga bentuk rumus tersebut makan pencarian panjang sisi untuk segitiga siku-siku dapat dilakukan dengan mudah. Sebagai contoh, berikut ini ada sebuah soal dan pembahasannya.
Soal:
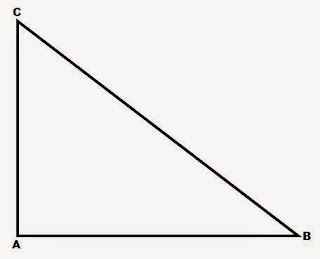
Diketahui segitiga siku-siku ABC dengan panjang sisi AB = 10 cm dan panjang sisi BC = 10 cm. Berapakah panjang sisi lainnya pada segitiga tersebut?
Jawab:
Dari soal tersebut, sudah diketahui sisi datar (AB) = 6 cm dan sisi miring (BC) = 10 cm. Sisi lainnya yang dimaksud adalah sisi tegak (AC). Untuk mencari sisi AC, rumus yang dipakai adalah rumus tipe kedua, yaitu x2 = z2 - y2
Berikut ini penyelesaiaannya:
AC2 = BC2 - AB2
= 102 - 62
= 100 - 36
= 64
Jadi nilai AC2 adalah 64 dan hasil dari panjang sisi AC adalah √64 yaitu sebesar 8 cm. Sampai disini hasil perhitungan untuk mencari sisi tegak (AC) sudah selesai dengan hasil panjang sisi AC adalah 8 cm.
Demikianlah ulasan mengenai Mapel Matematika tentang Rumus pitagoras segitiga siku-siku beserta contohnya. Semoga ulasan ini dapat dipahami dan dimengerti oleh pembaca semua.